Political Methodology

My work in political methodology has focused on machine learning, Bayesian nonparametric estimation, and methods for measurement of latent concepts in social science data.

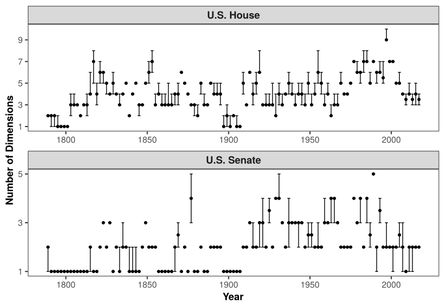
Dimensionality is a key concept in the social science literature; it is a proxy for the complexity of behaviors under simplified theories of utility based decision-making.  In studies of legislative behavior, dimensionality is an important measure in the debate of issue-based voting vs. party control.  In most applications of ideal point estimation, dimensionality is either assumed to be unidimensional or empirically tested using subjective post-hoc tests.  My work demonstrates that current tests can be misleading and are unable to distinguish statistically small, but important, dimensions from statistical noise.    

Using novel advancements in machine learning related to feature discovery, I show that proper statistical methods for uncovering dimensionality exist and provide information about the true dimensionality within a data set.   I demonstrate that the beta process and the corresponding Indian Buffet Process dictate priors that are useful for estimation of dimensionality in many corners of political science, including roll call voting, survey scaling, and treaty negotiation.  

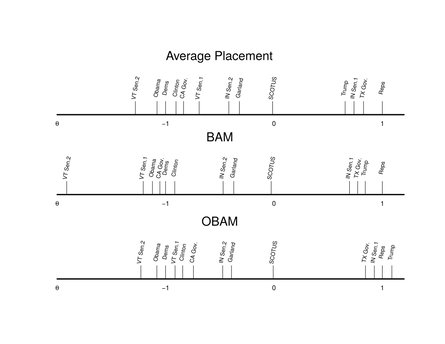
 Measurement models in the social sciences similarly require assumptions about the level of measurement for the observed data.  In many applications, latent variables are measured using data from discrete scales retrieved from surveys.  A common practice to correct for individual-level biases in survey answers is to use Aldrich-McKelvey scaling to create survey answers that are de-biased.  This approach commonly treats survey data as continuous responses and estimates the latent variable under this assumption.  My work (with Erin Cikanek and Hwayong Shin) demonstrates that this assumption can lead to incorrect inferences about both individual-level biases and the

placements of elites derived from survey responses.  We introduce a novel discrete-level scaling procedure, OBAM, that allows for survey response scaling under arbitrary discrete DGPs using copula.  This method is general and produces new insights about the links between bias in survey responses and polarization in the American public.

Clustering is another important unsupervised learning technique in the social sciences.  While mixture models are commonly used in the literature, there has been little work which explores how nonparametric cluster estimation can create new information about important social science data sets.  One approach which yields significant benefit is merging the standard ideal point model with the clustering model - an approach which finds ideal points of individuals and discovers groups within the data.  Often, groups are theoretically more

interesting and this approach can discover groups by examining departures from the underlying utility model that underlies ideal point estimation methods.  An extension of this method seeks to also discover linkages between groups - sets of observations that demonstrate conditional dependence.  Generative models of hierarchical clustering are a budding area in machine learning research and provide methods for discovering these kinds of relationships.  My work proposes a method for discovering hierarchies in latent variables via an   infinite hierarchical factor analysis model.

Political Institutions

My work is geared towards answering questions related to the ideal point model and measurement in observational social science data.  However, this work is directly applicable to analysis of other complex data types, such as text and images.

My work on political institutions explores the relationship between formal models of legislative voting, empirical tests of these theories, and the influence of measurement on assessments of political phenomena.

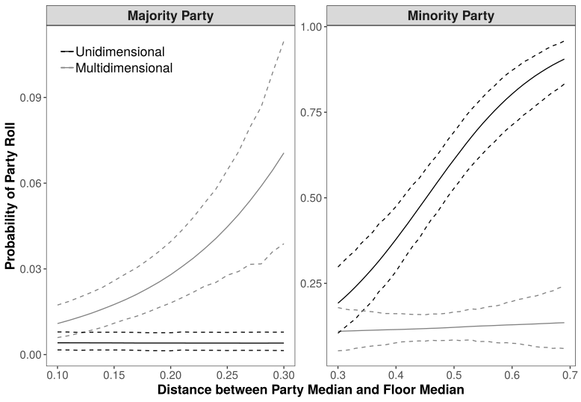
Empirical tests that seek to provide evidence for formal theories of legislative voting often rely on ideal point measurements to capture the many complexities of legislators' preferences.  Commonly, theories are tested using unidimensional ideal points.  This assumption inherently assumes that behavior beyond the first dimension of ideal point estimates is noise and unimportant for describing legislative decision making.  My work demonstrates the importance of dimensionality by showing that theories related to agenda control and pivotal 

voters are mediated by the dimensionality of a vote.  These results demonstrate that much of the interesting action that occurs in legislative voting is captured by dimensions beyond the first and inclusion of these dimensions in theories of voting is necessary for fully understanding how issue-based voting influences decision making and measures that utilize ideal point estimates.

Ideal point models typically scale items at the individual level, but seek to answer questions about political groups using individual-level measures.  Rather than scaling at this level and applying prior knowledge about the groups that exist, clustered ideal points can provide information about the role of parties and coalitions in legislative voting that exist beyond preconceived groups.  My work using clustered ideal point estimation demonstrates that there are many cleavages that exist in legislative voting, breaks that exist within and across parties.  Similarly, it shows the sets of issues that create these divisions. 

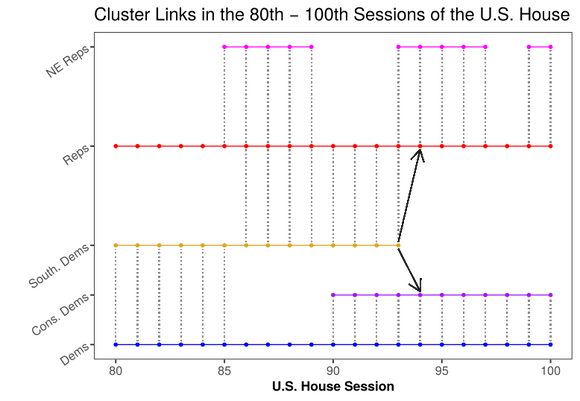
One question of interest to legislative scholars is the role that groups have played in the evolution of the U.S. Congress.  Understanding how party has influenced votes and the ways in which political groups have changed over time provides insight into the inner-workings of legislative decision making.  Using infinite hierarchical factor analysis, I show empirical evidence that party is not always the dominant decision making criteria for voters.  Examining the Southern Democratic coalition from the 1900s shows evidence that simply using party labels can lead to improper conclusions about the role of party over time.

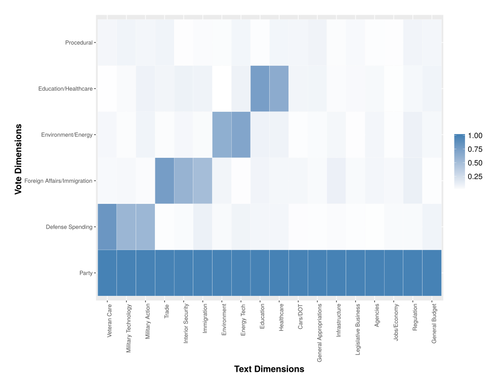
Roll call scaling typically only utilizes observed votes to scale data and interprets ideal points using this information.  Theories of issue-based voting contend that legislators cast votes conditional on the topic of a vote and other pressures that may influence vote outcomes.  One way to allow ideal points to account for potential issue based voting is to jointly scale the text associated with a vote and the votes, themselves.  Ideal points in this context then are explicitly linked to both vote outcomes and the context of the vote.  My work with dependent beta processes demonstrates a technique that allows for this joint scaling and provides ideal point estimates that can be directly interpreted in terms of the underlying text related to a vote.